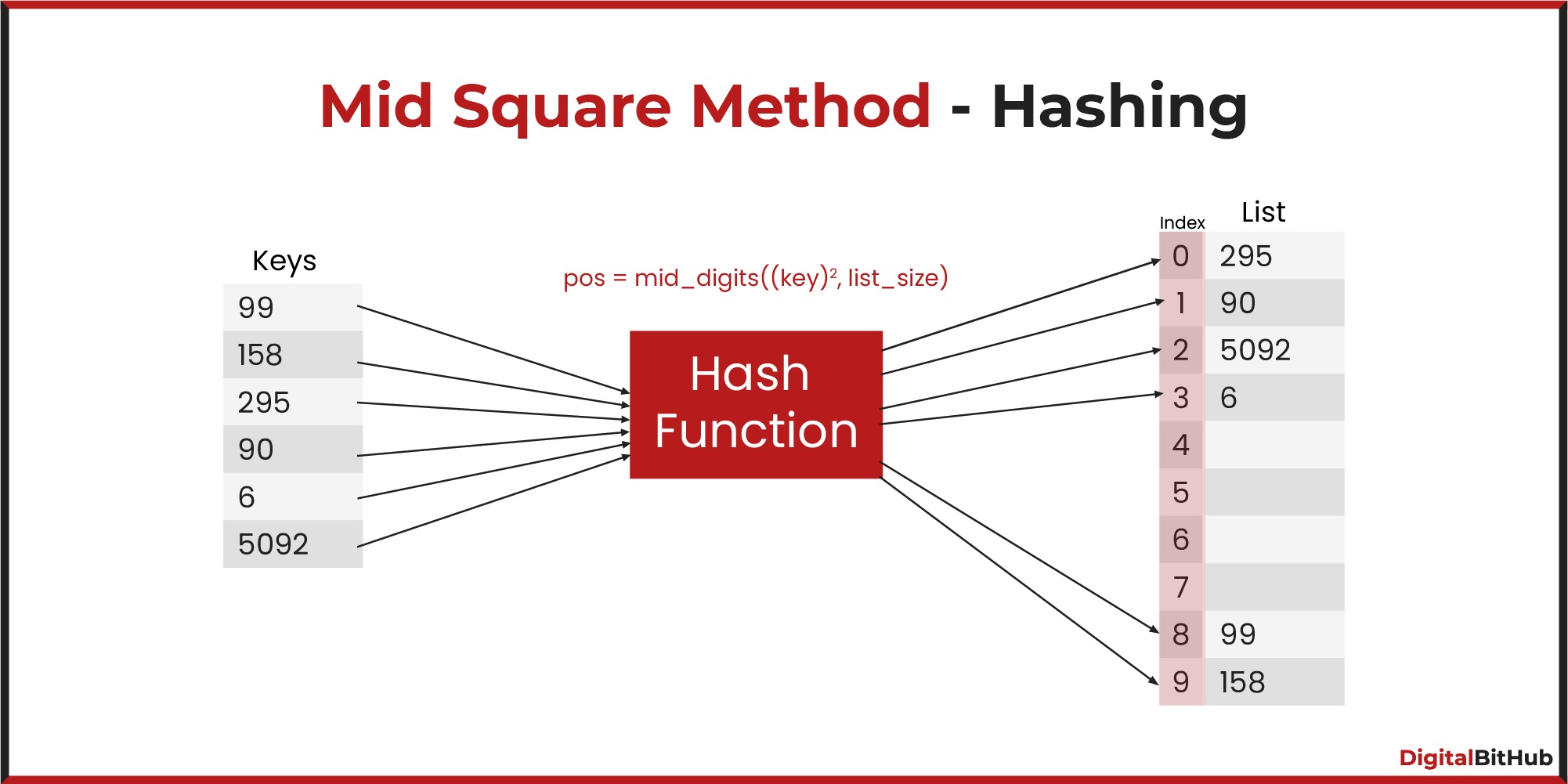
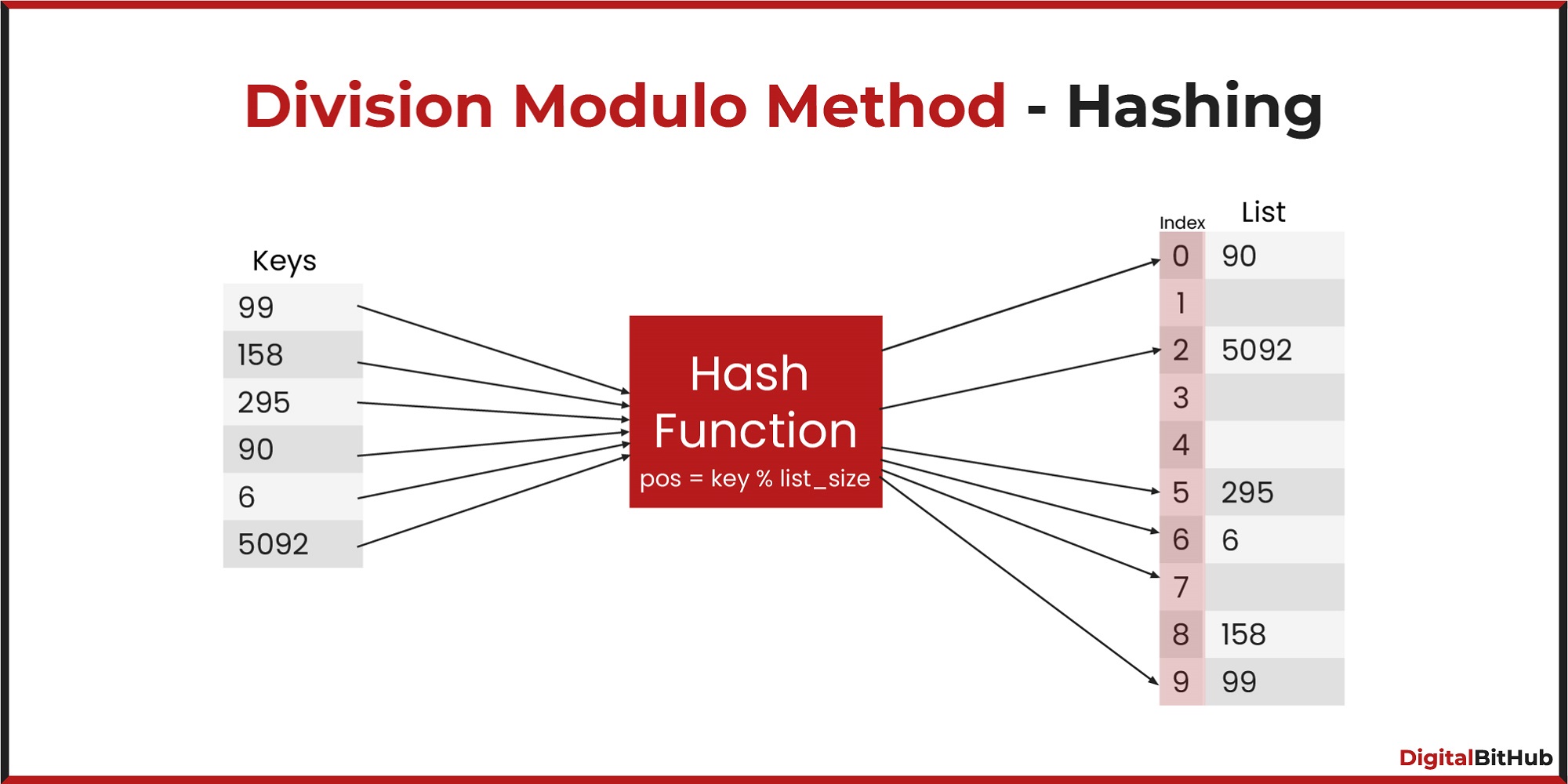
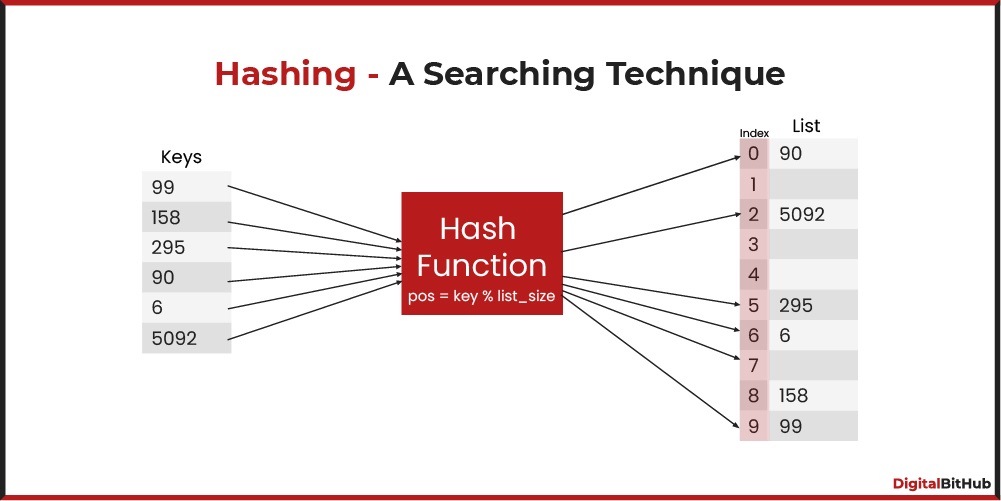
Consider a hash table of size 10 with indices {0, 1,..., 9}, with the hash function

h(x) = 3x (mod 10),

where linear probing is used to handle collisions. The hash table is initially empty and then the following sequence of keys is inserted into the hash table: 1, 4, 5, 6, 14, 15. The indices where the keys 14 and 15 are stored are, respectively

A.

2 and 5

B.

2 and 6

C.

4 and 5

D.

4 and 6

Solution:

We are given:

  • Hash table size: 10

  • Hash function: h(x) = (3x) mod 10

  • Collision resolution: Linear Probing

  • Keys inserted in order: 1, 4, 5, 6, 14, 15

🔍 Step-by-step Insertion:

🔹 Insert 1:

  • h(1)=3×1mod  10=3h(1) = 3 \times 1 \mod 10 = 3

  • Index 3 is free → insert at index 3

🔹 Insert 4:

  • h(4)=3×4mod  10=12mod  10=2h(4) = 3 \times 4 \mod 10 = 12 \mod 10 = 2

  • Index 2 is free → insert at index 2

🔹 Insert 5:

  • h(5)=3×5mod  10=15mod  10=5h(5) = 3 \times 5 \mod 10 = 15 \mod 10 = 5

  • Index 5 is free → insert at index 5

🔹 Insert 6:

  • h(6)=3×6mod  10=18mod  10=8h(6) = 3 \times 6 \mod 10 = 18 \mod 10 = 8

  • Index 8 is free → insert at index 8

🔹 Insert 14:

  • h(14)=3×14mod  10=42mod  10=2h(14) = 3 \times 14 \mod 10 = 42 \mod 10 = 2

  • Index 2 → occupied (by 4)

  • Linear probing → try index 3 → occupied (by 1)

  • Try index 4 → free → insert at index 4

🔹 Insert 15:

  • h(15)=3×15mod  10=45mod  10=5h(15) = 3 \times 15 \mod 10 = 45 \mod 10 = 5

  • Index 5 → occupied (by 5)

  • Try index 6 → free → insert at index 6

✅ Final answer:

14 → index 4, 15 → index 6

Correct option: (D) 4 and 6