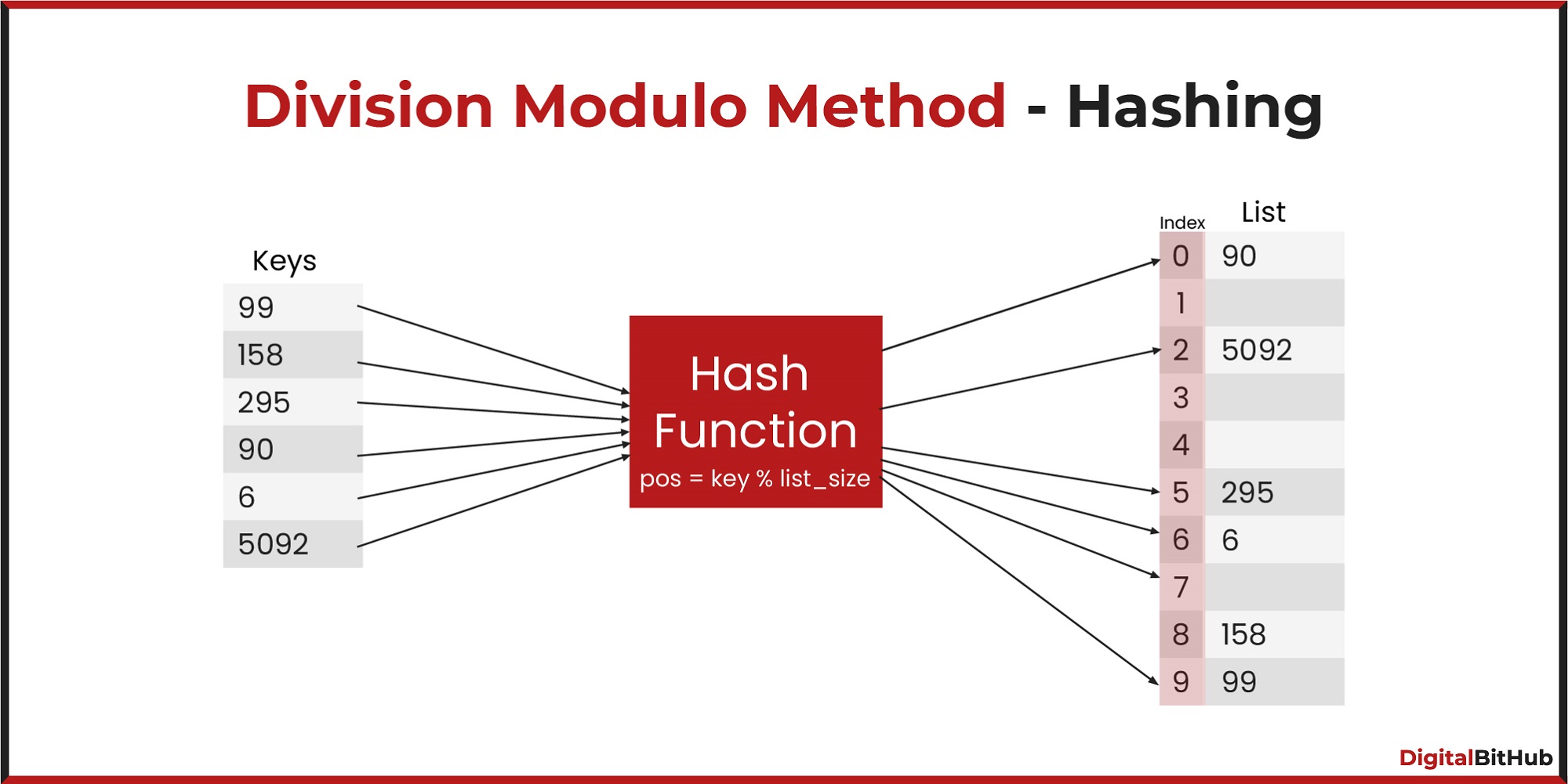
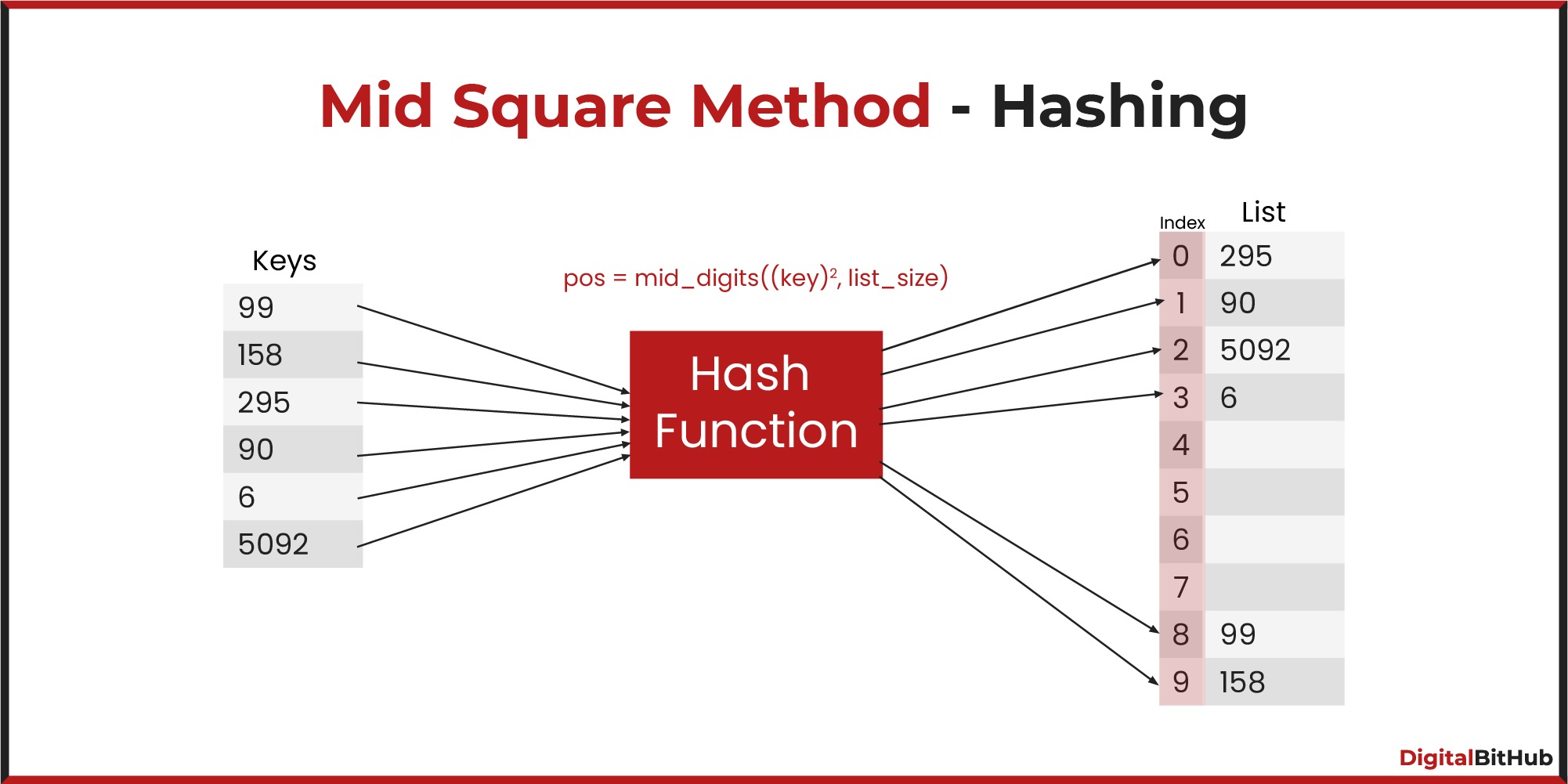
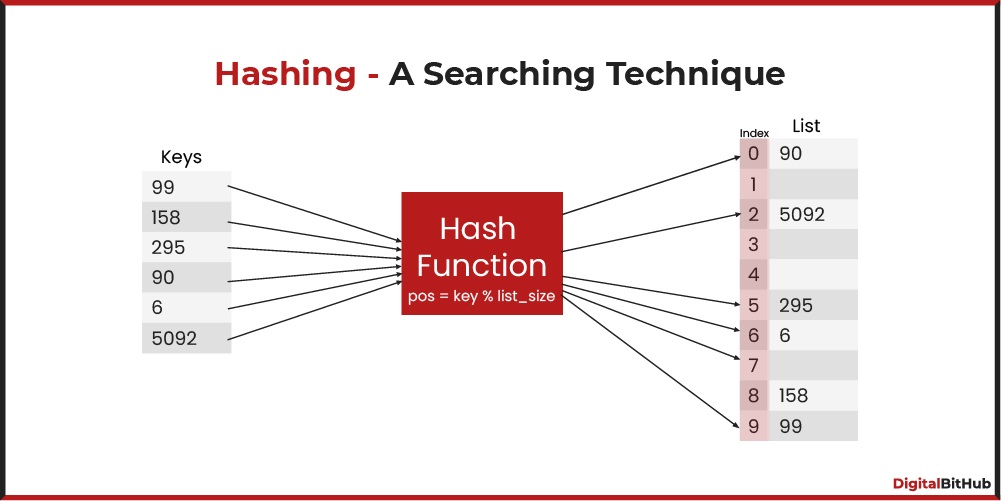
Division Modulo Method is the simplest method of hashing. In this method, we divide the element with the size of the hash table and use the remainder as the index of the element in the hash table.
Example 1:
Size of Hash Table (m) = 1000 (0 - 999)
Suppose we want to calculate the index of element x, where x = 123789456
index =123789456 mod 1000
= 456
we store the element x at position 456 in the hash table.
Example 2:
m = 8 (0 - 7) ⇒ 23
x = 10100101 (In Binary)
index = 10100101 mod 23 ⇒ 101 ⇒ 5
Example 3:
m = 2k
x = 101001011011101101 (In Binary)
Index will be the k L.S.B (Least Significant Bits).
if k = 4, then the index will be 1101
Problem with Division Modulo Method
There is one problem with this method, even if the element contains 1 lac bits, it will use only k least significant bit for the index.
Example 4:
m = 24
x = 1010111011101010000010......101101 (In Binary)
Index = 1101
In example 3 and example 4 calculated index value is the same (4 LSB). Due to this, collision will occur.
What is Collision
Collision in hashing is when two or more elements are fighting for the same slot in the hash table. In simple terms, we can say that If the hash function returns the same index for more than one element then the collision will occur.
Solution to the problem
- Don't pick hash table size (m) exactly the power of 2, because if m = 2k then HashFunction(m) = k LSB always.
- Pick hash table size (m) prime number, and make sure the value is not close to 2k.