- For any problem, if the answer is yes or no, then that problem is known as a decision problem otherwise it is an optimization problem.
- For any problem, if the algorithm is possible to solve that problem, then it is decidable problem.
There are three problems in Finite Automata
- Emptiness Problem
- Finiteness Problem
- Equivalence Problem
Emptiness Problem
The emptiness problem in Finite Automata is to decide whether the given automata are accepting empty language or not.
There is an Algorithm available to check the emptiness of Finite Automata.
- Step 1: Select those states which are not reachable from the initial state, delete those states and transitions. Using DFS or BFS.
- Step 2: In the remaining Finite Automata, if at least one final state then it is accepting non-empty language otherwise empty language.
Conclusion: The emptiness problem of finite automata is decidable and decision problem.
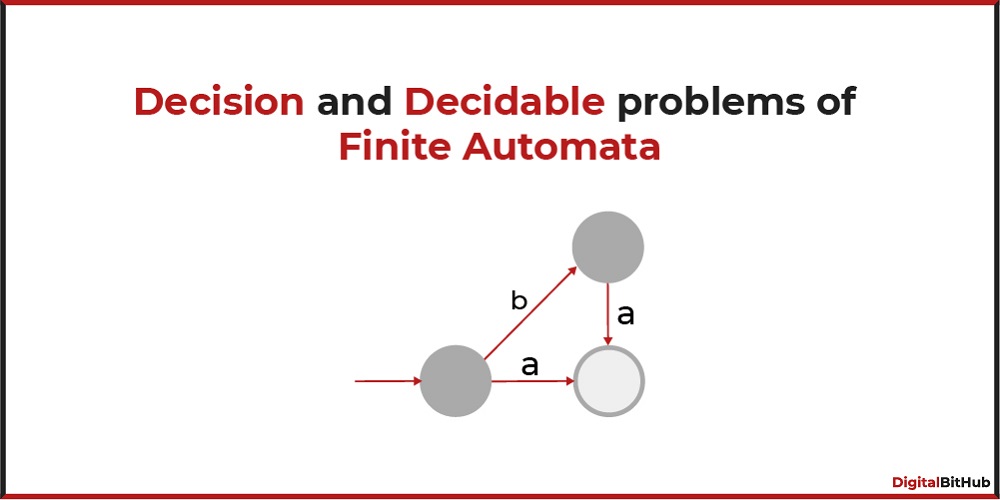
Example: Consider a Finite Automata

Given FA is accepting empty language. There is no final state in reachable states.
Finiteness Problem
The finiteness problem in Finite Automata is to decide whether the given automata is accepting finite language or infinite language.
There is an Algorithm available to check the finiteness of Finite Automata.
- Step 1: Select those states which are not reachable from the initial state, delete those states and transitions. Using DFS or BFS.
- Step 2: In the remaining Finite Automata, if any state from which we cannot reach the final state, delete those states and transitions.
- Step 3: In the remaining Finite Automata, if at least one cycle is available then it is accepting infinite language otherwise finite language.
Conclusion: The finiteness problem of finite automata is decidable and decision problem.
Example: Consider a Finite Automata

After applying the first 2 steps the resultant Finite Automata is

Loops exist in the resultant finite automata, hence accepting infinite language.
Equivalence Problem
The equivalence problem in Finite Automata is to decide whether the given two automata are accepting the same language or not.
There is an Algorithm available to check the equivalence of given two Finite Automata.
- Step 1: Create a transition table for given FAs.
- Step 2: If any entry of the table contains the final state of one automaton and the non-final state of other automata then the given FAs are not accepting the same language.
Conclusion: The equivalence problem of finite automata is decidable and decision problem.
Example: Consider the following two Finite Automata

The transition table for the above two automata is

Transition table entries are in form of (A, B), where A is the state from Finite Automata 1 and B is the state from Finite Automata 2.
NF means Non-Final State
F means Final State
Above transition table does not contain any conflicting entry hence the given FAs are accepting the same language.